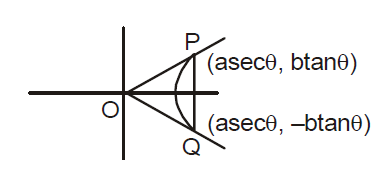
Q. If $PQ$ is a double ordinate of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ such that $\Delta OPQ$ is equilateral, $O$ being the centre. Then the eccentricity e satisfies
WBJEEWBJEE 2016
Solution:
$\because \Delta OPQ$ is equilateral,
$OP = PQ$
$\Rightarrow a^{2}\,sec^{2}\,\theta+b^{2}\,tan^{2}\,\theta=\left(2b\,tan\,\theta\right)^{2}$
$\Rightarrow a^{2}\,sec^{2}\,\theta+3b^{2}\,tan^{2}\,\theta$
$\Rightarrow sin^{2}\,\theta= \frac{a^{2}}{3b^{2}}$
Now, $sin^{2}\,\theta <1$
$\Rightarrow \frac{a^{2}}{3b^{2}} >1$
$\Rightarrow \frac{b^{2}}{a^{2}}>\frac{1}{3} \Rightarrow 1+\frac{b^{2}}{a^{2}} > \frac{4}{3} \Rightarrow e^{2}>\frac{4}{3} \Rightarrow e> \frac{2}{\sqrt{3}}$