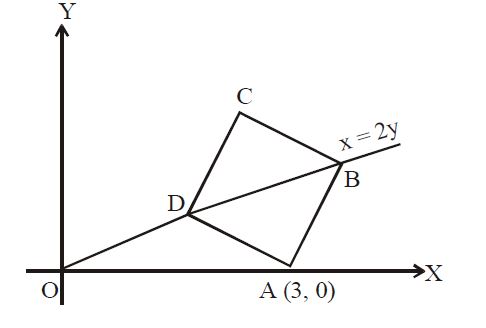
Q. If one of the diagonals of a square is along the line x = 2y and one of its vertices is (3, 0), then its sides through this vertex are given by the equations
Straight Lines
Solution:
Clearly the point (3, 0) does not lie on the diagonal x = 2y. Let m be the slope of a side passing through (3, 0). Then its equation is
$y - 0 = m (x - 3) \,....(i)$
Since the angle between a diagonal and a side of a square is $\frac{\pi}{4}$. Therefore angle between
$x=2y\, \& \, y-0=m\left(x-3\right)$ is also $\frac{\pi}{4}$
Consequently, $tan \frac{\pi}{4}=\pm\frac{m-\frac{1}{2}}{1+\frac{m}{2}} \Rightarrow m=3, -\frac{1}{3}$
$\therefore $ from $\left(i\right)$, we get the required equations
$y=3\left(x-3\right) \Rightarrow y-3x+9=0$ or
$y=-\frac{1}{3}\left(x-3\right) \Rightarrow 3y+x-3=0$