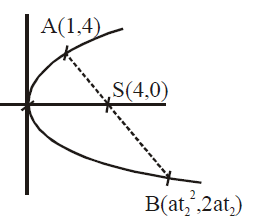
Q. If one end of a focal chord of the parabola, $y^2 = 16x$ is at $(1, 4),$ then the length of this focal chord is
Solution:
$y^2 = 4ax = 16x \Rightarrow a = 4$
A(1,4) $\Rightarrow $ 2.4.t$_1$ = 4 $\Rightarrow \, t_1 \, = \, \frac{1}{2}$
$\therefore \, $ length of focal chord $ = s \bigg(t + \frac{1}{t}\bigg)^2$
$= 4 \bigg(\frac{1}{2} + 2\bigg)^2 \, = 4, \frac{25}{4} \, = 25$