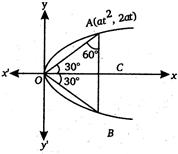
Q. If OAB is an equilateral triangle inscribed in the parabola $ {{y}^{2}}=4ax $ with O as the vertex, then the length of the side of the $ \Delta \,\,OAB $ is
J & K CETJ & K CET 2008
Solution:
In $ \Delta OCA,\,\,\,\tan {{30}^{o}}=\frac{AC}{OC} $
$ \Rightarrow $ $ \frac{1}{\sqrt{3}}=\frac{2at}{a{{t}^{2}}} $
$ \Rightarrow $ $ t=2\sqrt{3} $
Again in $ \Delta \,OCA, $
$ OA=\sqrt{O{{C}^{2}}+A{{C}^{2}}} $
$ =\sqrt{{{(a{{t}^{2}})}^{2}}+{{(2at)}^{2}}} $
$ =\sqrt{{{[{{(2\sqrt{3})}^{2}}]}^{2}}{{a}^{2}}+4{{a}^{2}}{{(2\sqrt{3})}^{2}}} $
$ =\sqrt{144\,{{a}^{2}}+48{{a}^{2}}}=\sqrt{192\,{{a}^{2}}} $
$ =8\sqrt{3}\,a $