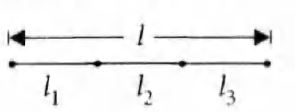Q. If $n_1, n_2$ and $ n_3$ are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency $n$ of the string is given by
AIPMTAIPMT 2014Waves
Solution: