Question

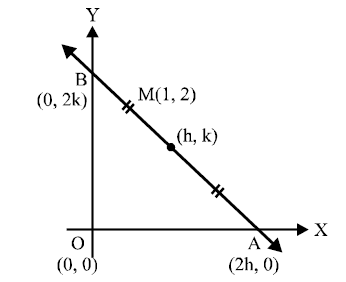
If $\ell, m , n$ are three consecutive odd integers then the family of lines $\ell x - my + n =0$ passes through a fixed point $M ( a , b )$
Number of straight lines passing through $M ( a , b )$ and making an area of $2$ square unit with coordinate axes in the first quadrant, is equal to

• A. 1
• B. 0
• C. 2
• D. 4

Answer 1

Answer: (B)

Let $\ell=2 r +1, m =2 r +3, n =2 r +5$
$\therefore 2 r ( x - y +1)+( x -3 y +5)=0$
$\Rightarrow $ line passes through fixed point $(1,2)$
So, $a =1, b =2 $
$\Rightarrow M (1,2)$
(i) We have $\frac{x}{2 h}+\frac{y}{2 k}=1$ (intercept form)
$\Rightarrow \frac{1}{2 x}+\frac{2}{2 y}=1$
$ \Rightarrow y+2 x=2 x y $
$\Rightarrow 2 x+y-2 x y=0$
(ii) Let slope of line be ' $m$ ' as $m<0$.
$\therefore $ Equation of line $( y -2)= m ( x -1)$ (given)
(ii) Let slope of line be ' $m$ ' as $m<0$.
$\therefore $ Equation of line $( y -2)= m ( x -1)$ (given)

Now, area of $(\Delta OAB =2) ($ given $)$
$\Rightarrow \frac{1}{2}(2- m ) \frac{( m -2)}{ m }=2 $
$\Rightarrow ( m -2)^{2}=-4 m $
$\Rightarrow m ^{2}-4 m +4=-4 m$
$\Rightarrow m ^{2}+4=0$
So, no real value of $m$ exist.