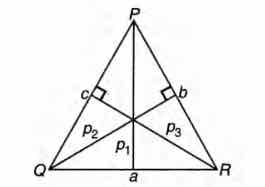
Question

If in a $\triangle$ PQR, sin P, sin Q, sin R are in AP, then

• A. the altitudes are in AP
• B. the altitudes are in HP
• C. the medians are in GP
• D. the medians are in AP

Answer 1

Answer: (B)

By the law of sine rule,
$\frac{a}{ sin \ P } = \frac{b}{ sin \ Q} = \frac{ c}{ sin \ R } = k $ [ say]
Also, $ \frac{1}{2}, ap_1 = \triangle \Rightarrow \frac{ 2 \\triangle }{\alpha} = p_1$
$\Rightarrow p_1 = \frac{2 \triangle }{ k \ sin \ P }$
Similarly, $ p_2 = \frac{ 2 \triangle }{ k \ sin \ Q } \ and \ p_3 = \frac{2 \triangle }{ k \ sin \ R }$
Since, sin P, sin Q and sin R are in AP, hence $p_1, p_2, p_3$ are in HP.