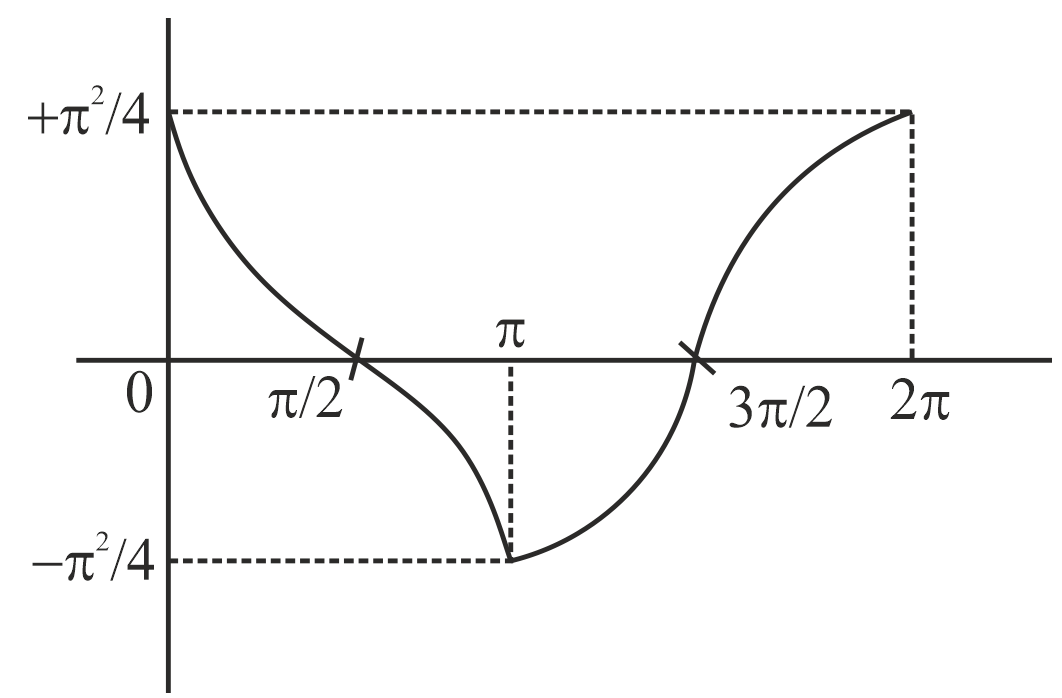
Question

If $f(x)=\left(\frac{\pi}{2}-\cos ^{-1}(\cos x)\left(\frac{\pi}{2}-\sin ^{-1}(\sin x)\right)\right)$, where $x \in[-2 \pi, 2 \pi]$, then the number of integers in the range of $f(x)$ is

Answer 1

Periodic function with period $=2\pi $
$f\left(x\right)=\left(sin\right)^{- 1}\left(cos x\right)\cdot \left(cos\right)^{- 1}\left(sin x\right)$
$f\left(x\right)=\begin{cases} \left(\frac{\pi }{2} - x\right)^{2} & ,x\in \left[0 , \frac{\pi }{2}\right] \\ -\left(\frac{\pi }{2} - x\right)^{2} & ,x\in \left(\frac{\pi }{2} , \pi \right) \\ \left(x - \frac{\pi }{2}\right)\left(x - \frac{3 \pi }{2}\right) & ,x\in \left[\pi , \frac{3 \pi }{2}\right] \\ \left(x - \frac{3 \pi }{2}\right)\left(\frac{5 \pi }{2} - x\right) & ,x\in \left[\frac{3 \pi }{2} , 2 \pi \right] \end{cases}$

$R_{f}\in \left[- \frac{\pi ^{2}}{4} , \frac{\pi ^{2}}{4}\right]$