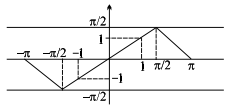
Q. If $f(x)=\operatorname{cosec}^{-1}(\operatorname{cosec} x)$ and $\operatorname{cosec}\left(\operatorname{cosec}^{-1} x\right)$ are equal functions then maximum range of values of $x$ is
Inverse Trigonometric Functions
Solution:
$y =\operatorname{cosec}^{-1}(\operatorname{cosec} x ) ; x \in R -\{ n \pi, n \in I \} ; y \in[-\pi / 2,0) \cup(0, \pi / 2]$
and $ y =\operatorname{cosec}\left(\operatorname{cosec}^{-1} x \right) ;| x | \geq 1 ;| y | \geq 1$
$\therefore $ range of value of $x y \in\left[-\frac{\pi}{2},-1\right] \cup\left[1, \frac{\pi}{2}\right]$