Q.
If $f(x)=\frac{1}{x}$, then which of the following statements is /are true?
I. $\displaystyle\lim _{x \rightarrow 0^{+}} f(x)=+\infty$
II. $\displaystyle\lim _{x \rightarrow 0^{-}} f(x)=-\infty$
III. $\displaystyle\lim _{x \rightarrow 0} f(x)$ does not exist.
Continuity and Differentiability
Solution:
To analyse the function $f(x)=\frac{1}{x}$ near $x=0$. We follow the usual trick of finding the value of the function at real numbers close to 0 . Essentially we are trying to find the right hand limit of $f$ at 0 . We tabulate this in the following table
$x$
$1$
$0.3$
$0.2$
$0.1 = 10^{-1}$
$0.01 = 10^{-2}$
$0.001 = 10^{-3}$
$10^{-n}$
$f(x)$
$1$
$3.333......$
$5$
$10$
$100 = 10^2$
$1000 = 10^3$
$10^n$
We observe that as $x$ gets closer to 0 from the right, the value of $f(x)$ shoots up higher. This may be rephrased as the value of $f(x)$ may be made larger than any given number by choosing a positive real number very close to 0 .
In symbols, we write
$\displaystyle\lim _{x \rightarrow 0^{+}} f(x)=+\infty$
(to be read as the right hand limit of $f(x)$ at 0 is plus infinity). We wish to emphasise that $+\infty$ is not a real number and hence the right hand limit of $f$ at 0 does not exist (as a real number).
Similarly, the left hand limit of $f$ at 0 may be found. The following table is self explanatory
$x$
$-1$
$-0.3$
$-0.2$
$- 10^{-1}$
$-10^{-2}$
$- 10^{-3}$
$-10^{-n}$
$f(x)$
$-1$
$-3.333......$
$-5$
$-10$
$- 10^2$
$- 10^3$
$-10^n$
From the Table II, we deduce that the value of $f(x)$ may be made smaller than any given number by choosing a negative real number very close to 0 . In symbols, we write
$\displaystyle\lim _{x \rightarrow 0^{-}} f(x)=-\infty$
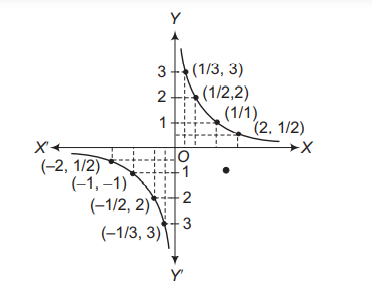
(to be read as the left hand limit of $f(x)$ at 0 is $-\infty$ ). Again, we wish to emphasise that $-\infty$ is not a real number and hence the left hand limit of $f$ at 0 does not exist (as a real number). The graph of the reciprocal function given in figure is a geometric representation of the above mentioned facts.
| $x$ | $1$ | $0.3$ | $0.2$ | $0.1 = 10^{-1}$ | $0.01 = 10^{-2}$ | $0.001 = 10^{-3}$ | $10^{-n}$ |
| $f(x)$ | $1$ | $3.333......$ | $5$ | $10$ | $100 = 10^2$ | $1000 = 10^3$ | $10^n$ |
| $x$ | $-1$ | $-0.3$ | $-0.2$ | $- 10^{-1}$ | $-10^{-2}$ | $- 10^{-3}$ | $-10^{-n}$ |
| $f(x)$ | $-1$ | $-3.333......$ | $-5$ | $-10$ | $- 10^2$ | $- 10^3$ | $-10^n$ |