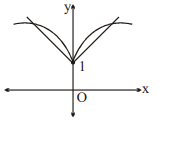
Question

If $f$ is a positive real valued differentiable function satisfying the functional rule $f^2(x+y)=f^2(x)+f^2(y)-2 \sqrt{x}-2 \sqrt{y}+2 \sqrt{x+y}-1$ for all $x, y \geq 0$ such that $\underset{h \rightarrow 1}{\text{Lim}} \frac{f(h)-2}{h-1}=\frac{1}{2}$, then find the number of solution(s) of the equation $\frac{f(|x|)}{\lambda|x|+1}=1(\lambda >0)$.

Answer 1

$f^2(x+y)=f^2(x)+f^2(y)-2 \sqrt{x}-2 \sqrt{y}+2 \sqrt{x+y}-1$
Partially differentiating w.r.t. $x$

$2 f(x+y) f^{\prime}(x+y)=2 f(x) f^{\prime}(x)-\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{x+y}}$
Putting $x =1$
$2 f(1+y) f^{\prime}(1+y)=2 f(1) f^{\prime}(1)-1+\frac{1}{\sqrt{1+y}} $
$2 f(1+y) f^{\prime}(1+y)=2 \cdot 2 \cdot \frac{1}{2}-1+\frac{1}{\sqrt{1+y}} $
$2 f(1+y) f^{\prime}(1+y)=1+\frac{1}{\sqrt{1+y}}$
$2 f(x) f^{\prime}(x)=1+\frac{1}{\sqrt{x}} \Rightarrow(f(x))^2=x+2 \sqrt{x}+C$
$\text { Putting } x=1, C=1 $
$\Rightarrow f(x)=\sqrt{x}+1 .$