Q.
If f and $g$ are the functions whose graphs are shown, let $P(x)=f(x) g(x), Q(x)=\frac{f(x)}{g(x)}$ and $C(x)=f(g(x))$.
The value of $\left( P ^{\prime}(2)- C ^{\prime}(2)\right) Q ^{\prime}(2)$ equals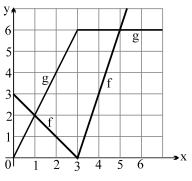
Continuity and Differentiability
Solution: