Q.
If each diode in figure has a forward bias resistance of $25\,\Omega$ and infinite resistance in reverse bias, The values of the current
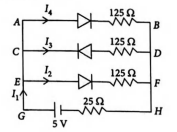
Semiconductor Electronics: Materials Devices and Simple Circuits
Solution: