Question

If $b >a$, then the equation $(x-a)(x-b)$ $-1=0$ has

• A. both roots in $[a, b]$
• B. both roots in $(-\infty, a)$
• C. both roots in $(b, \infty)$
• D. one root in $(-\infty, a)$ and other in $(b, \infty)$.

Answer 1

Answer: (D)

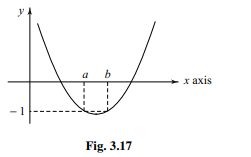
Graph of $y=(x-a)(x-b)-1$ is given in Fig. 3.17.
It is a parabola which open upwards. Also, $y< 0$ for $x=a$ and $x=b$.
$\therefore y=(x-a)(x-b)-1$ meets the $x$-axis at two points once in $(-\infty, a)$ and once in $(b, \infty)$. Thus, one root lies in $(-\infty, a)$ and one in $(b, \infty)$