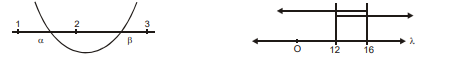Question

If $\alpha, \beta$ be the roots of $4 x ^2-16 x +\lambda=0$, where $\lambda \in R$, such that $1< \alpha< 2$ and $2< \beta< 3$, then the number of integral values of $\lambda$ is

• A. 5
• B. 6
• C. 2
• D. 3

Answer 1

Answer: (D)

$4 x^2-16 x+\lambda=0$
$f(1)>0$ and $f(2)<0 f(3) >0$

$4-16+\lambda >0 $
$ \lambda >12 $
$ f(2)=16-32+\lambda <0 $
$ \lambda <16 $
$ f(3)=36-48+\lambda >0 $
$ \lambda >12 $
$ 12 < \lambda< 16$
So $\lambda=13,14,15$ has 3 integral solutions.