1. Tardigrade
  2. Question
  3. Physics
  4. If a slab of insulating material 4× 10-3 m thick is introduced between the plates of a parallel plate capacitor, the separation between plates has to be increased by 3.5× 10-3 m to restore the capacity to original value. The dielectric constant of the material will be

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

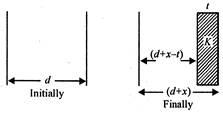
Q. If a slab of insulating material $ 4\times {{10}^{-3}} $ m thick is introduced between the plates of a parallel plate capacitor, the separation between plates has to be increased by $ 3.5\times {{10}^{-3}} $ m to restore the capacity to original value. The dielectric constant of the material will be

AMUAMU 1999

Solution:

: Capacity of a parallel plate capacitor $ =\frac{{{\varepsilon }_{0}}KA}{d} $ Initially, $ {{C}_{1}}=\frac{{{\varepsilon }_{0}}A}{d} $ Let separation be increased by $ x $ .
Finally, $ {{C}_{2}}=\frac{{{\varepsilon }_{0}}A}{(d+x-t)+\frac{t}{K}} $ Since $ {{C}_{1}}={{C}_{2}}, $ $ d=d+x-t+\frac{t}{k}; $ $ t-x=\frac{t}{K} $ $ K=\frac{t}{t-x}=\frac{4\times {{10}^{-3}}}{4\times {{10}^{-3}}-3.5\times {{10}^{-3}}}=\frac{4}{4-3.5}=8 $

Solution Image