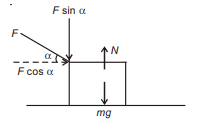
Question

If a pushing force making an angle $\alpha$ with horizontal is applied on a block of mass $m$ placed on horizontal table and angle of friction is $\beta$, then minimum magnitude of force required to move the block is

• A. $\frac{m g \sin \beta}{\cos [\alpha-\beta]}$
• B. $\frac{m g \sin \beta}{\cos [\alpha+\beta]}$
• C. $\frac{m g \sin \beta}{\sin [\alpha+\beta]}$
• D. $\frac{m g \cos \beta}{\cos [\alpha-\beta]}$

Answer 1

Answer: (B)

Angle of friction is $\beta$
$\Rightarrow \mu=\tan \beta$
$N=m g +F \sin \alpha$
To just move the block
$F \cos \alpha=\mu N$
$F \cos \alpha=\tan \beta(m g+ F \sin \alpha)$
$F(\cos \alpha-\tan \beta \sin \alpha)=m g \tan \beta$
$F(\cos \alpha \cos \beta-\sin \alpha \sin \beta)=m g \sin \beta$
$F=\frac{m g \sin \beta}{\cos (\alpha+\beta)}$