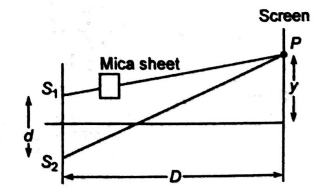
Question

If a mica sheet of thickness $t$ and refractive index $\mu$ is placed in the path of one of interfering beams in a double slit experiment, then displacement of fringes will be :

• A. $ \frac{D}{d}\mu t $
• B. $ \frac{D}{d}(\mu -1)t $
• C. $ \frac{D}{d}(\mu +1)t $
• D. $ \frac{D}{d}({{\mu }^{2}}-1)t $

Answer 1

Answer: (B)

We can realise the situation as shown. Geometric path difference between $S_{2} P$ and $S_{1} P$ is
$\Delta x_{1}=S_{2} P-S_{1} P=\frac{y d}{D}$

where $d$ is distance between the slits and $D$ the distance between source and screen.
Path difference produced by the mica sheet
$\Delta x_{2}=(\mu-1) t$
Therefore, net path difference between the two rays is
$\Delta x=\Delta x_{1}-\Delta x_{2}$
or $\Delta x=\frac{y d}{D}-(\mu-1) t$
For $n$th maxima on upper side,
$\Delta x=n \lambda$
$\therefore \frac{y d}{D}-(\mu-1) t=n \lambda$
$\therefore y=\frac{n \lambda D}{d}+\frac{(\mu-1) t D}{d}$
Earlier it was $\frac{n \lambda D}{d}$.
$\therefore $ Displacement of fringes $=\frac{(\mu-1) t D}{d}$