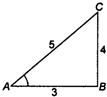
Question

If $ A $ lies in the second quadrant and $ 3\tan A+4=0 $ , then value of $ 2\cot A-5\cos A+\sin A $ is equal to:

• A. $ -53/10 $
• B. $ -7/10 $
• C. $ 7/10 $
• D. $ 23/10 $

Answer 1

Answer: (D)

In second quadrant $\tan , \cot , \cos$ are negative and sin are positive.
Given that, $3 \tan A+4=0 $
$\Rightarrow \tan A=-\frac{4}{3}$
Since, $A$ lies in Ilnd quadrant
$\therefore \cot A=-\frac{3}{4}, \cos A=-\frac{3}{5}, \sin A=\frac{4}{5}$
$\therefore 2 \cot A-5 \cos A+\sin A$
$=2\left(-\frac{3}{4}\right)-5\left(-\frac{3}{5}\right)+\frac{4}{5}=-\frac{3}{2}+3+\frac{4}{5}$
$=\frac{-15+30+8}{10}=\frac{23}{10}$