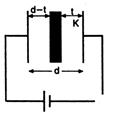
Q. If a dielectric plate of thickness t is placed between the plates of a parallel plate capacitor of plate distance d, the capacitance becomes half of the original value. The dielectric constant of the plate will be:
VMMC MedicalVMMC Medical 2002
Solution:
The capacitor of the capacitance without placing the dielectric plate is given by $ C=\frac{{{\varepsilon }_{0}}A}{d} $ ?(1)
When the dielectric plate of dielectric constant K and thickness t is inserted between the parallel plates of a capacitor, then it becomes the series combination of two capacitors as shown in figure, so the equivalent capacitance $ {{C}_{eq}} $ is $ {{C}_{eq}}=\frac{C}{2}=\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}} $ Here, $ {{C}_{1}}=\frac{{{\varepsilon }_{0}}A}{d-t} $ and $ {{C}_{2}}=\frac{K{{\varepsilon }_{0}}A}{t} $ or $ \frac{C}{2}=\frac{\left( \frac{{{\varepsilon }_{0}}A}{d-t} \right)\times \left( \frac{K{{\varepsilon }_{0}}A}{t} \right)}{{{\varepsilon }_{0}}A\left\{ \frac{1}{d-t}+\frac{K}{t} \right\}}=\frac{K{{\varepsilon }_{0}}A}{t+(d-t)K} $ or $ \frac{C}{2}=\frac{K{{\varepsilon }_{0}}A}{t+(d-t)K} $ As $ C=\frac{{{\varepsilon }_{0}}A}{d} $ or $ {{\varepsilon }_{0}}A=Cd $ or $ \frac{C}{2}=\frac{KCd}{t+(d-t)K} $ or $ t+(d-t)K=2Kd $ or $ K\{-(d-t)+2d\}=t $ or $ K=\frac{t}{d+t} $