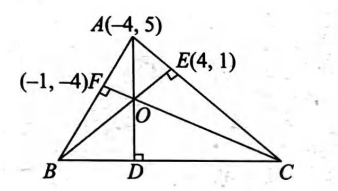
Question

If $A D, B E$ and $C F$ are the altitudes of a triangle $A B C$ whose vertex $A$ is the point $(-4,5)$. The coordinates of the points $E$ and $F$ are $(4,1)$ and $(-1,-4)$ respectively, then equation of $B C$ is

• A. $3 x-4 y-28=0$
• B. $4 x+3 y-28=0$
• C. $3 x-4 y+28=0$
• D. $x+2 y+7=0$

Answer 1

Answer: (A)

Slope of $A F=\frac{5-(-4)}{-4+1}=\frac{9}{-3}=-3$
$\therefore$ Slope of $C F=\frac{1}{3}$
$\therefore$ Equation of $C F$ is $x-3 y-11=0$ (i)
Slope of $A E=\frac{5-1}{-4-4}=\frac{4}{-8}=-\frac{1}{2}$
$\therefore$ Slope of $B E=2$
$\therefore$ Equation of $B E$ is $2 x-y-7=0$ (ii)
Solving (i) and (ii), we get point $O=(2,-3)$
Equation of $A C$ is $x+2 y-6=0$ (iii)
Solving (i) and (iii) we get point $C(8,-1)$
Also slope of $A O$ is $-4 / 3$
$\therefore$ Slope of $B C$ is $3 / 4$
$\therefore$ Equation of $B C$ is $3 x-4 y-28=0$