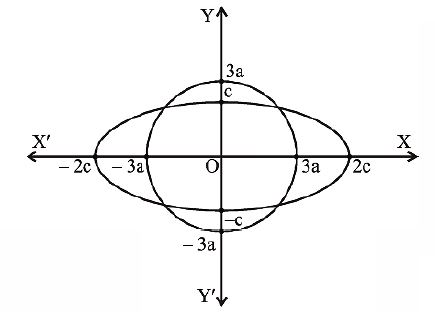
Q. If $a$ and $c$ are positive real numbers and the ellipse $\frac{x^{2}}{4c^{2}}+\frac{y^{2}}{c^{2}} = 1$ has four distinct points in common with the circle $x^2 + y^2 = 9a^2$, then
Solution:
Radius = $3a$
Length of major axis = $4c$
Now, (Radius) < (Half of the length of major axis)
$3a < 2c$
$9a^2 < 4 c^2$
$9ac - 9a^2 > 9ac - 4c^2$
$9ac - 9a^{2} - 2c^{2} > 9ac - 6c^{2}\quad\quad\ldots\left(i\right)$
Again $3 a < 2c$
$\Rightarrow 9ac<6c^{2}$
$\Rightarrow 9ac-6c^{2}<0\quad\quad\ldots \left(ii\right)$
From $\left(i\right)$ and $\left(ii\right)$,
$9ac - 9a^{2} - 2c^{2} > 0$