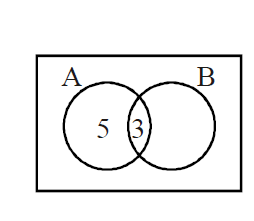
Q. If $A$ and $B$ are any two events such that $P(A) = \frac {2}{5}$ and $P(A \cap B) = \frac {3}{20}$ then the conditional probability, $P(A|(A' \cup B'))$,where $A'$ denotes the complement of $A$, is equal to :
Solution:
$P\left(A\right)=\frac{2}{5}=\frac{8}{20}; P\left(A\cap B\right)=\frac{3}{20}$
$P\left(\overline{A\cup B}\right)=1-\frac{3}{20}$
$\Rightarrow P\left(\bar{A}\cup\bar{B}\right)=\frac{17}{20}$
$A\cap\left(A'\cup B'\right)$
$=A-\left(A\cap B\right)$
$\therefore P\left(A-\left(A\cap B\right)\right)=\frac{5}{20}$
$\therefore P\left(A/\left(A'\cap B'\right)\right)=\frac{P\left(A-\left(A\cap B\right)\right)}{P\left(\bar{A}\cup\bar{B}\right)}=\frac{5}{17}$