Q. If $\left(a, a^{2}\right)$ falls inside the angle made by the lines $y=\frac{x}{2}, x>\, 0$ and $y=3x, x>\, 0, \quad$ then a belongs to:
AIEEEAIEEE 2006Straight Lines
Solution:
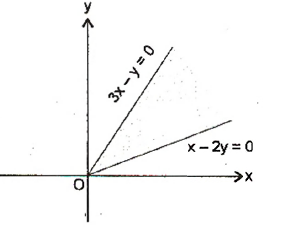
The graph of equations $x-2y = 0 $ and $3x - y = 0$ is as shown in the figure. Since given point $\left(a, a^{2}\right)$ lies in the shaded region.
Then $a-2a^{2} <\, 0$ and $3a-a^{2} >\, 0$
$\Rightarrow \, a \in \left(-\infty, 0\right) \cup\left(\frac{1}{2}, \infty\right)$
and $ a \in \left(0,3\right) \Rightarrow a \in \left(\frac{1}{2}, 3\right)$