Question

If $0 < x < 1$, then $\sqrt{1+x^2}[\{x cos(cot^{-1}x)$
$+sin(cot^{-1}x)\}^2-1]^{1/2}$ is equal to

• A. $\frac{x}{\sqrt{1+x^2}}$
• B. $x$
• C. $x\,\sqrt{1+x^2}$
• D. $\sqrt{1+x^2}$

Answer 1

Answer: (C)

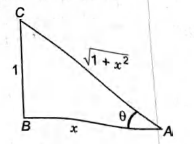
We have, 0 < x < 1
Let $ \, \, \, \, \, \, \, \, \, cot^{-1}x=\theta$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, cot \theta=x$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, sin\theta=\frac{1}{\sqrt{1+x^2}}=sin(cot^{-1}x)$
and $ \, \, \, \, \, \, \, \, \, \, \, \, cos \theta =\frac{x}{\sqrt{1+x^2}}=cos(cot^{-1}x)$
$Now, \, \sqrt{1+x^2}[\{x cos (cot^{-1}x)+sin(cot^{-1}x)\}^2 -1]^{1/2}$
$ \, \, \, \, \, \, \, \, \, \, \, =\sqrt{1+x^2}\bigg[\bigg(x\frac{x}{\sqrt1+x^2}+\frac{1}{\sqrt{1+x^2}}\bigg)^2-1\bigg]^{1/2}$
$ \, \, \, \, \, \, \, \, \, \, \, =\sqrt{1+x^2}\bigg[\bigg(x\frac{1+x^2}{\sqrt1+x^2}\bigg)^2-1\bigg]^{1/21}$
$ \, \, \, \, \, \, \, \, \, \, \, =\sqrt{1+x^2}[1+x^2-1]^{1/2}=x\sqrt{1+x^2}$