Q.
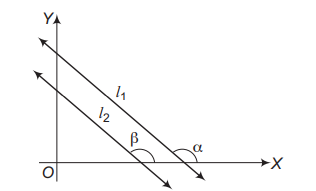
I. Two non-vertical lines $l_1$ and $l_2$ are parallel, if and only if their slopes are equal.
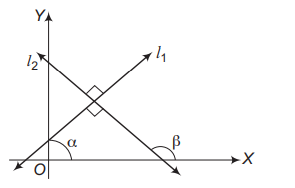
II. Two non-vertical lines $l_1$ and $l_2$ are perpendicular to each other, if and only if their slopes are negative reciprocals of each other.
Straight Lines
Solution: