Q.
Graph of $f ( x )= ax ^2+ bx + c , a , b , c \in R , a \neq 0$ is shown in the adjacent figure. If area of rectangle $O A B C=18$ sq. units ( $B$ is the vertex of the parabola) and sum of the roots of the equation $f(x)$ $=0$ is 12 , then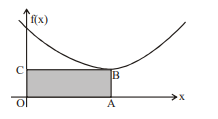
Complex Numbers and Quadratic Equations
Solution: