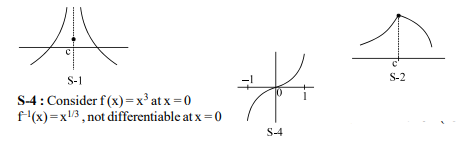Q.
Give the correct order of initials $T$ or $F$ for following statements. Use $T$ if statement is true and $F$ if it is false.
Statement-1: If $f: R \rightarrow R$ and $c \in R$ is such that $f$ is increasing in $(c-\delta, c)$ and $f$ is decreasing in $(c, c+\delta)$ then $f$ has a local maximum at $c$. Where $\delta$ is a sufficiently small positive quantity.
Statement-2 : Let $f :( a , b ) \rightarrow R , c \in( a , b )$. Then $f$ can not have both a local maximum and a point of
inflection at $x = c$.
Statement-3: The function $f ( x )= x ^2| x |$ is twice differentiable at $x =0$.
Statement-4 : Let $f :[ c -1, c +1] \rightarrow[ a , b ]$ be bijective map such that $f$ is differentiable at $c$ then $f ^{-1}$ is also differentiable at $f ( c )$.
Application of Derivatives
Solution:
S-1 : f must be continuous $\Rightarrow$ false $S -2 x = c$ is local max.but not inflection point $\Rightarrow$ True