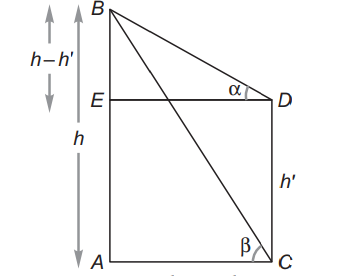
Question

From the top of a hill $h$ metres high the angles of depressions of the top and the bottom of a pillar are $\alpha$ and $\beta$ respectively. The height (in metres) of the pillar is

• A. $\frac{h(\tan \beta-\tan \alpha)}{\tan \beta}$
• B. $\frac{h(\tan \alpha-\tan \beta)}{\tan \alpha}$
• C. $\frac{h(\tan \beta+\tan \alpha)}{\tan \beta}$
• D. $\frac{h(\tan \beta+\tan \alpha)}{\tan \alpha}$

Answer 1

Answer: (A)

Let $A B$ be a hill whose height is $h$ metres and $C D$ be a pillar of height $h^{'}$ metres. In $\Delta E D B$
$\tan \alpha=\frac{h-h^{'}}{E D}\,\,\,...(i)$
and in $\Delta A C B$,

$\tan \beta=\frac{h}{A C}=\frac{h}{E D}\,\,\,...(ii)$
Eliminate ED from Eqs. (i) and (ii),
we get
$\tan \alpha=\frac{h-h^{'}}{\frac{h}{\tan \beta}}$
$\Rightarrow h \frac{\tan \alpha}{\tan \beta}=h-h^{'}$
$\Rightarrow h^{'}=\frac{h(\tan \beta-\tan \alpha)}{\tan \beta}$