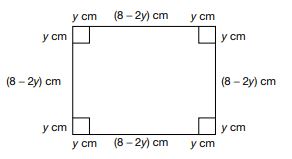
Question

From each corner of a square sheet of side $8 cm$, a square of side $\gamma cm$ is cut. The remaining sheet is folded into a cuboid. The minimum possible volume of the cuboid formed is $M$ cubic $cm$. If $y$ is an integer, then find $M$.

• A. 32
• B. 18
• C. 36
• D. 12

Answer 1

Answer: (D)

Length $=$ Breadth $=(8-2 \gamma) cm$ and height $=\gamma cm$.
Its volume $=(8-2 \gamma)(8-2 \gamma) \gamma$
$=(8-2 \gamma)^2 y$ cubic $cm$.
$8-2 y >0$, i.e., $y< 4$ and $y$ is an integer.
$\therefore y=1$ or 2 or 3 .
Among these values of $\gamma$, volume is minimum when $y=3$.
When $y=3$, volume $=12 cm ^3$.
$\therefore M=12$.