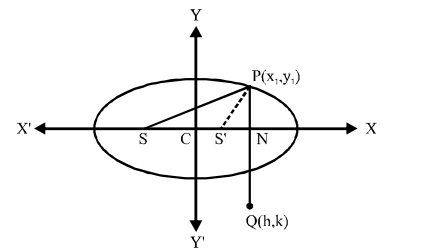
Question

From any point $P$ lying in the first quadrant on the ellipse $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1, P N$ is drawn perpendicular to the major axis and produced at $Q$ so that $NQ$ equals to $PS$, where $S$ is a focus. Then the locus of $Q$ is

• A. $5 y-3 x-25=0$
• B. $3 x+5 y+25=0$
• C. $3 x-5 y-25=0$
• D. none of these

Answer 1

Answer: (B)

$a^{2}=25$ and $b^{2}=16$
or $e =\sqrt{1-\frac{16}{25}}=\frac{3}{5}$
Let point Q be (h, k), where k $ < 0$.
Given that $k = SP = a +ex_{1}$,
where $P \left( x _{1}, y _{1}\right)$ lies on the ellipse,
Then,
$| k |= a + eh \left(\text { As } x _{1}= h \right)$
or $-y=a+e x$
or $3 x+5 y+25=0$