Q. From any point on the circle $ {{x}^{2}}+{{y}^{2}}={{a}^{2}}, $ two tangents are drawn to the circle $ {{x}^{2}}+{{y}^{2}}={{a}^{2}}si{{n}^{2}}\alpha , $ then angle between them is
Rajasthan PETRajasthan PET 2002
Solution:
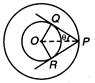
Let PQ and PR are two tangents and point P is
on the circle
$ {{x}^{2}}+{{y}^{2}}={{a}^{2}} $ with coordinates $ (a\cos t,a\sin t) $ and $ \angle OPQ=\theta $
Now, $ PQ= $ length of tangent drawn from the point P to the circle $ {{x}^{2}}+{{y}^{2}}={{a}^{2}}si{{n}^{2}}\alpha $
$ \therefore $ $ PQ=\sqrt{{{a}^{2}}{{\cos }^{2}}t+{{a}^{2}}{{\sin }^{2}}t-{{a}^{2}}{{\sin }^{2}}\alpha } $
$ =\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}\alpha } $
$ =a\cos \alpha $ and $ OQ= $ radius of the circle $ {{x}^{2}}+{{y}^{2}}={{a}^{2}}si{{n}^{2}}\alpha $
$ \Rightarrow $ $ OQ=a\text{ }sin\,\alpha $
$ \therefore $ $ \tan \theta =\frac{OQ}{QP}=\frac{a\sin \alpha }{a\cos \alpha }=\tan \alpha $ $ \theta =\alpha $
$ \therefore $ Angle between both the tangents $ =2\alpha $