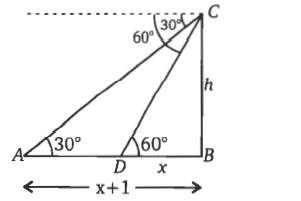
Question

From an aeroplane flying, vertically above a horizontal road, the angles of depression of two consecutive stone on the same side of the aeroplane are observed to be 30$^\circ$ and 60$^\circ$ respectively. The height at which the aeroplane is flying in km is

• A. $2$
• B. $\frac {2}{\sqrt {3}}$
• C. $\frac {\sqrt {3}}{2}$
• D. $\frac {4}{\sqrt {3}}$

Answer 1

Answer: (C)

Let the distance of two consecutive stones are $x, x + 1$.
In $\Delta BCD$,

$\tan\,60^{\circ} = \frac{h}{x}$
$ \Rightarrow \, x = \frac{h}{\sqrt{3}}\,\,\,\,\dots(i)$
In $\Delta ABC$,
$\tan \, 30^{\circ} = \frac{h}{x+1}$
$ \Rightarrow \,\frac{1}{\sqrt{3}} = \frac{h}{x+1}$
$ \Rightarrow \, \frac{h}{\sqrt{3}} + 1 = \sqrt{3} h$ (From (i))
$\Rightarrow \, \frac{2h}{\sqrt{3}} = 1 $
$ \Rightarrow \, h = \frac{\sqrt{3}}{2} \, km$