Question

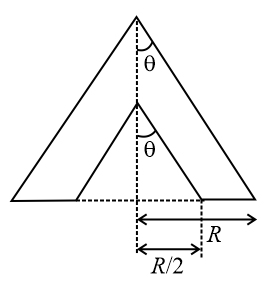
From a uniform solid cone of base radius $R$ and height $H$ , a symmetric cone of base radius $\frac{R}{2}$ is removed as shown.
Then the center of mass is shifted by $\frac{H}{n}.$ Find the value of $n$ .

Answer 1

When symmetric cone is removed then center of mass can be calculated by this relation
$y_{cm}=\frac{m_{1} y_{1} - m_{2} y_{2}}{m_{1} - m_{2}}$ ........(i)
Where $m_{1}$ and $m_{2}$ are masses, $y_{1}$ and $y_{2}$ are center of masses for original and removed cone respectively. We take origin $'O'\left(0 , 0\right)$ as coordinate of center of mass of original cone.

$\triangle ABC$ and $\triangle DFG$ are similar triangles, so for $\triangle DFG$ , $\frac{EG}{ED}=\frac{EC}{BG}$ , for $\triangle BEC$
$\frac{R}{2 \times H '}=\frac{R}{H}$
$\Rightarrow H'=\frac{H}{2}$
So, center of mass $\left(y_{2}\right)$ for smaller cone is
$\frac{1}{4}\left(\frac{H}{2}\right)=\frac{H}{8}$
For same density, mass of cone depends on its volume.
Mass of bigger cone is $m_{1}$ (let) $=\frac{1}{3}\pi R^{2}H$
Mass of smaller cone is $m_{2}$ (let) $=\frac{1}{3}\pi \left(\frac{R}{2}\right)^{2}\times \frac{H}{2}$
$\Rightarrow m_{2}=\frac{1}{8}\left(\frac{1}{3} \left(\pi R\right)^{2} H\right)=\frac{m_{1}}{8}$
Putting values of $m_{1}$ , $y_{1}=0$ and $m_{2}=\frac{m_{1}}{8},y_{2}=\frac{H}{8}$ in equation (i)
$y_{cm}=\frac{m_{1} \times 0 - \frac{m_{1}}{8} \times \frac{H}{8}}{m_{1} - \frac{m_{1}}{8}}$
Put, $y _{ cm }=\frac{ H }{ n }$ in above equation, in above equation,
$\frac{H}{n}=\frac{H}{56}$
$\Rightarrow n=56$