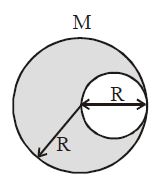
Q. From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre ?
Solution:
$I_{Total disc } = \frac{MR^2}{2}$
$M_{Removed} = \frac{M}{4} (Mass \propto area) $
$I_{removed} $ (about same Perpendicular axis)
$ = \frac{M}{4} \frac{(R /2)^2}{2} + \frac{M}{4} (\frac{R}{2})^2 = \frac{3MR^2}{32} $
$ I_{Remaing disc } = I_{Total} - I_{Removed} $
$ = \frac{MR^2}{2} - \frac{3}{32} MR^2 = \frac{13}{32} MR^2$