Q.
From a circular disc of radius $R$ and mass $9M$, a small disc of radius $R / 3$ is removed from the disc, the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through $O$ is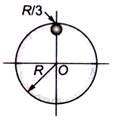
IIT JEEIIT JEE 2005System of Particles and Rotational Motion
Solution: