Question

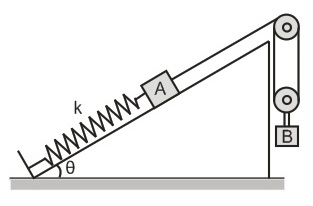
Friction is absent everywhere and the threads, spring and pulleys are massless. If $m_{A}=m_{B}=m$ , then the angular frequency of the system for small oscillations will be

• A. $\sqrt{\frac{\text{2k}}{\text{4m}}}$
• B. $\sqrt{\frac{\text{4k}}{\text{5m}}}$
• C. $\sqrt{\frac{\text{6k}}{\text{7m}}}$
• D. $\sqrt{\frac{\text{8k}}{\text{5m}}}$

Answer 1

Answer: (B)

Let $x_{0}$ be the extension in the spring in equilibrium. Then
equilibrium of $A$ and $B$ given,
$ T = kx _{0}+ mg \sin \theta $
and $ 2 T = mg$
Here, $T$ is the tension in the string. Now, suppose $A$ is further displaced by a distance $x$ from its mean position and $v$ be its speed at this moment. Then $B$ lowers by $\frac{x}{2}$ and speed of $B$ at this instant will be $\frac{v}{2}$ Total energy of the system in this position will be,
$ E =\frac{1}{2} k \left(x+x_{0}\right)^{2}+\frac{1}{2} m _{ A } v ^{2}+\frac{1}{2} m _{ B }\left(\frac{ v }{2}\right)^{2}+ m _{ A } gh _{ A }- m _{ B } gh _{ B } $
or $E =\frac{1}{2} k \left(x+x_{0}\right)^{2}+\frac{1}{2} mv ^{2}+\frac{1}{8} mv ^{2}+ mgx \sin \theta- mg \frac{x}{2}$
or $ E =\frac{1}{2} k \left(x+x_{0}\right)^{2}+\frac{5}{8} mv ^{2}+ mgx \sin \theta- mg \frac{x}{2}$
Since, $E$ is constant,
$ \frac{ dE }{ dt }=0 $
or $ 0= k \left(x+x_{0}\right) \frac{ d x}{ dt }+\frac{5}{4} mv \left(\frac{ dv }{ dt }\right)+ mg (\sin \theta)\left(\frac{ d x}{ dt }\right)-\frac{ mg }{2}\left(\frac{ d x}{ dt }\right)$
Substituting, $ \frac{ d x}{ dt }= v$
$ \frac{ dv }{ dt }=a $
and $ k x_{0}+ mg \sin \theta=\frac{ mg }{2}$
[From equations (i) and (ii)]
We get, $ \frac{5}{4} m a=- k x$
Since, $ a \propto-x$
Motion is simple harmonic, time period of which is,
$ \begin{array}{l} T =2 \pi \sqrt{\left|\frac{x}{a}\right|}=2 \pi \sqrt{\frac{5 m }{4 k }} \\ \omega=\frac{2 \pi}{ T }=\sqrt{\frac{4 k }{5 m }} \end{array} $