1. Tardigrade
  2. Question
  3. Physics
  4. Four resistances 5 Ω , 10 Ω, 15 Ω and 20 Ω are connected in a cyclic order so as to form an unbalanced Wheatstone's bridge. The bridge can be balanced by (i) connecting 25 Ω in series with 15 Ω (ii) connecting 12 Ω in parallel with 20 Ω

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

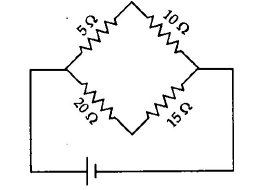
Q. Four resistances $5 \, \Omega , 10\, \Omega, 15\, \Omega$ and $20\, \Omega $ are connected in a cyclic order so as to form an unbalanced Wheatstone's bridge. The bridge can be balanced by
(i) connecting $25 \, \Omega $ in series with $15\, \Omega$
(ii) connecting $12 \, \Omega$ in parallel with $20 \, \Omega$

COMEDKCOMEDK 2011Current Electricity

Solution:

Given situation is shown in the figure.
(i) Connecting $25 \, \Omega $ in series with $15 \, \Omega$
Net resistance in the arm $= 25 + 15 = 40 \, \Omega$
$ \frac{5}{10} = \frac{20}{40}$ which is the required condition for balanced Wheat stone bridge.
(ii) Connecting $12 \, \Omega $ in parallel with $20 \, \Omega $
Net resistance ,$ = \frac{20 \times 12}{20 + 12} = \frac{15}{2} \Omega $
Hence, $\frac{5}{10} = \frac{7.5}{15} $ which is the required condition for balanced Wheat-stone bridge.

Solution Image