Q.
Four point charges (with equal magnitude of charge of $5\, C$; but with different signs) are placed at four corners of a square of side $10\, m.$ Assuming that the square is centered at the origin and the configuration of the charges are as given in the figure, the potential and the magnitude of electric field at the origin, respectively are [ Note : $k = \frac{1}{4 \pi \varepsilon_0}$]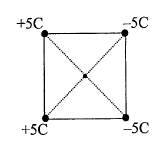
KEAMKEAM 2019
Solution:
