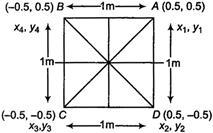
Q. Four particles, each of mass 1 kg, are placed at the corners of a square of side 1m in the X-Y plane. If the point of intersection of the diagonals of the square, is taken as the origin the coordinates of the centre of mass are
CMC MedicalCMC Medical 2014
Solution:
Given, $ {{m}_{1}}={{m}_{2}}={{m}_{3}}={{m}_{4}}=1\,kg $ $ AB=BC=CD=DA=1\,m $
Hence, the coordinates of A,B, C, D, are given in the figure from the relation for $ {{x}_{cm}} $ is $ {{x}_{cm}}=\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}+{{m}_{4}}{{x}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}} $ $ =\frac{1\times 0.5+1\times 0.5+1\,(-0.5)+1\times (-0.5)}{1+1+1+1}=0 $ $ {{y}_{cm}}=\frac{{{m}_{1}}{{y}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}+{{m}_{4}}{{y}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}} $ $ =\frac{1\times 0.5+1\times (-0.5)+1\times (-0.5)+1\times (0.5)}{1+1+1+1} $ $ =0 $