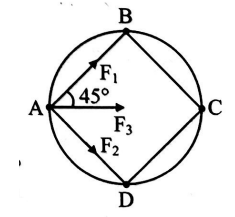
Q.
Four identical particles of mass $M$ are located at the corners of a square of side ' $a$ '. If each of them revolves under the influence of others gravitational field in a circular orbit circumscribing the square, their speed is found to be $Q$ times $\sqrt{\frac{G M}{a}}$. The value of $Q$ is_____.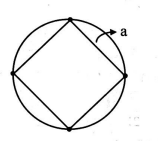
Gravitation
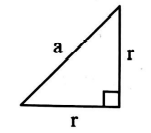
Solution: