Q.
Four identical mirrors are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint $M$ of mirror $AD$ and after two reflections reaches corner $D$. Then, angle $\theta$ must be
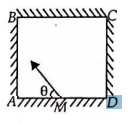
Ray Optics and Optical Instruments
Solution:
