Q.
Four holes of radius $R$ are cut from a thin square plate of side $4R$ and mass $M$ . The moment of inertia of the remaining portion about the $x$ -axis is
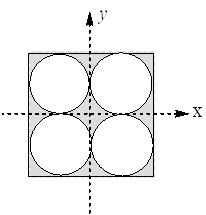
NTA AbhyasNTA Abhyas 2022
Solution: