Question

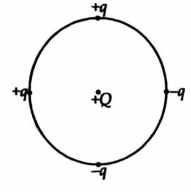
Four charges, $+q, +q, -q, -q $ are placed on the circumference of a circle of radius $r$. What is the force on the charge $+Q$ placed at the centre of the circle as shown in the figure?

• A. $\frac{1}{4\pi\varepsilon_{0}} \frac{Qq}{r^{2}}$
• B. $\frac{1}{4\pi\varepsilon_{0}} \frac{\sqrt{8}Qq}{r^{2}}$
• C. $\frac{1}{4\pi\varepsilon_{0}} \frac{ 8 Qq}{r^{2}}$
• D. $\frac{1}{4\pi\varepsilon_{0}} \frac{2 Qq}{r^{2}}$

Answer 1

Answer: (B)

Force on charge $Q$ due to charge $q$ at $A$,
$F_{1} = \frac{1}{4\pi\varepsilon_{0}} \frac{Qq}{r^{2}}$ along $AO$
Force on charge $Q$ due to charge $q$ at $B$,
$F_{2} = \frac{1}{4\pi\varepsilon_{0}} \frac{Qq}{r^{2}}$ along $BO$
Force on charge $Q$ due to charge $-q$ at $C$,
$F_{3} = \frac{1}{4\pi\varepsilon_{0}} \frac{Qq}{r^{2}}$ along $OC$
Force on charge $Q$ due to charge $-q$ at $D$,
$F_{4} = \frac{1}{4\pi\varepsilon_{0}} \frac{Qq}{r^{2}}$ along $OD$
$\left|F_{1}\right| = \left|F_{2}\right| = \left|F_{3}\right| = \left|F_{4}\right| = F $
The resultant force on charge $Q$ is
$F_{net} = \sqrt{\left(2F\right)^{2} + \left(2F\right)^{2} + 2\left(2F\right)\left(2F\right)cos 90^{\circ}} $
$= F\sqrt{8}$
$ = \frac{1}{4\pi\varepsilon_{0}}\frac{\sqrt{8}Qq}{r^{2}}$