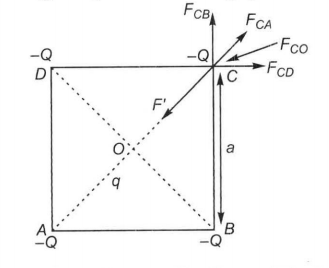
Q. Four charges equal to $-Q$ are placed at the four corners of a square and a charge $q$ is at its centre. lf the system is in equilibrium, the value of $q$ is
Solution:
The system is in equilibrium means the force experienced by each charge is zero. It is clear that charge placed at centre would be in equilibrium for any value of $q$, so we are considering the equilibrium of charge placed at at any corner.
$ F_{ CD} + F_{ CA} \, cos\, 45^\circ \, + F_{ CO} \, cos\, 45^\circ = 0 $
$\Rightarrow \frac{ 1}{ 4 \pi \varepsilon_0} . \frac{ ( - Q) \, ( - Q) }{ a^2 } + \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ ( - Q) \, ( - Q) }{ \sqrt 2 a^2 } \times \frac{ 1}{ \sqrt 2} $
$ + \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ ( - Q) q }{ ( \sqrt 2 a/ 2)^2 } \times \frac{ 1}{ 2} = 0 $
$\Rightarrow \frac{ 1}{ 4 \pi \varepsilon_0} . \frac{ ( Q^2 }{ a^2 } + \frac{ 1}{ 4 \pi \varepsilon_0} . \frac{ Q^2 }{ 2a^2 } . \frac{ 1}{ \sqrt 2}$
$ - \frac{ 1}{ 4 \pi \varepsilon_0} . \frac{ 2 Qq }{ a^2 } \times \frac{ 1}{ \sqrt 2} = 0 $
$\Rightarrow Q + \frac{ Q}{ 2 \sqrt 2} - \sqrt 2 q = 0 $
$\Rightarrow 2 \sqrt 2 Q + Q - 4 q = 0 $
4q = $ ( 2 \sqrt 2 + 1) Q $
q = $ \frac{ Q}{ 4 } ( 2+ 2 \sqrt 2)$