Q.
Force acting on a body varies with time as shown below. If initial momentum of the body is $\vec{p}$, then the time taken by the body to retain its momentum $\vec{p}$ again is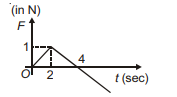
Laws of Motion
Solution:
