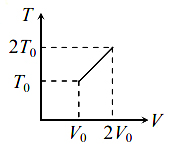Q.
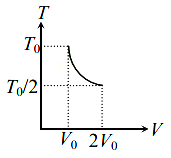
For two thermodynamic process temperature and volume, diagrams are drawn. In the first process, it is a straight line having initial and final coordinates as $\left(V_{0} , T_{0}\right)$ and $\left(2 V_{0} , 2 T_{0}\right)$ , whereas in second process it is a rectangular hyperbola having initial and final coordinates (V0, T0) and (2V0, T0/2). Then the ratio of work done in the two processes must be
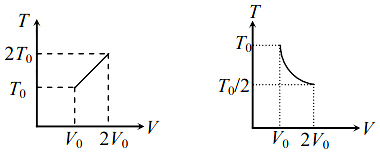
NTA AbhyasNTA Abhyas 2020Thermodynamics
Solution: