Q.
For the wave shown in figure, if its position shown is at $ 4{{l}_{0}}{{\cos }^{2}}\left( \frac{\pi y}{\beta } \right) $ . Then the equation of the wave is [when speed of wave, $ {{C}_{1}} $ ]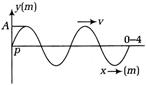
BVP MedicalBVP Medical 2015
Solution: