Q.
For the LCR circuit, shown here, the current is observed to lead the applied voltage. An additional capacitor $C ^{\prime}$, when joined with the capacitor C present in the circuit, makes the power factor of the circuit unity. The capacitor $C ^{\prime}$, must have been connected in parallel with C and has a magnitued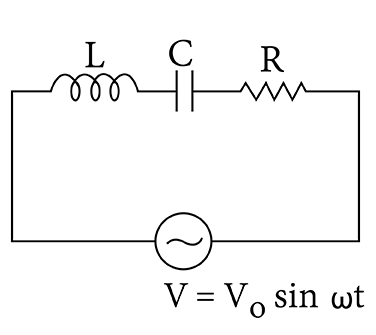
Solution: