Question

For the function $f (x) = x cos$ $ \frac{1}{x}, x \ge 1 $,

• A. for at least one $x$ in the interval
  $ [ 1, \infty) , \, f (x + 2) - f (x) < 2 $
• B. $lim_{ x \to \infty} f' (x) = 1 $
• C. for all $x$ in the interval $ [1, \infty), f (x + 2) - f (x) > 2$
• D. $f' (x)$ is strictly decreasing in the interval $[1, \infty)$

Answer 1

Answer: (B), (C), (D)

Given, f (x) = x cos $ \frac{1}{x}, x \ge 1 \Rightarrow f \, ' (x) = \frac{1}{x} \, sin \, \frac{1}{x} + cos \frac{1}{ x} $
$\Rightarrow $ f " (x) = - $ \frac{1}{x^3} \, cos \, \bigg( \frac{1}{x}\bigg)$
Now, $ lim_{ x \to \infty} $ f ' (x) = 0 + 1 = 1 $ \Rightarrow $ Option (b) is correct
Now, $ x \, \in [1, \infty) \Rightarrow \frac{1}{x} \in (0, 1] \Rightarrow $ f " (x) < 0
Option (d) is correct.
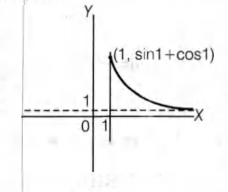
As f ' (1) = sin 1 + cos 1 > 1
f ' (x) is strictly decreasing and $ lim_{ x \to \infty} $ f ' (x) = 1
So, graph of f ' (x) is shown as below
Now, in
[ x, x + 2], x $ \in [1, \infty), $ f (x) is
continuous and differentiable
so by LMVT,
f ' (x) = $ \frac{ f (x + 2) - \, f (x)}{ 2}$
As, f' (x) > 1
For all x $ \in [1, \infty) $
$\Rightarrow \frac{ f (x + 2) - \, f (x)}{ 2} > 1 \Rightarrow $ f (x + 2) - f (x) > 2
For all x $ \in [1, \infty)$